Research

Dynamical systems are encountered within nature through various conformal representations ranging from physical phenomena such as turbulence to bacteria population dynamics to financial investment dynamics to the movement of extraterrestrial planets, etc. The common denominator in all these mutually exclusive examples is the dependence on time (either discrete or continuous) and the evolution of their respective degrees of freedom (DOFs) with time. However, the underlying governing equations that dictate this evolution aren’t always readily accessible or are computationally expensive endeavours. This necessitates the exploration of autonomous data-driven algorithms. There have been significant strides in the development of classical computing hardware and, in recent years, quantum computing hardware, which further accelerates the development of these algorithms. This is where the core of my research lies !

1. Data Assimilation and Probabilitic Inference

In practice it is often the case that we have uncertainties in both our information of the state of the system and as well as the global parameters that dictate the intrinsic physics of the system. Data Assimilation process hence can be utilized to improve our knowledge of both our state and parameters, however this process calls for reformulating our problem and augmenting our problem such that it account for both parameter-state estimation.

Generative AI - Denoising Diffusion Probabilistic Models (DDPMs)

The idea of Diffusion models is to generate unique samples from the original data distribution via a parametrized (neural network based) markov chain based networks trained using the concept variational inference through the modeling of dynamical system (Stochastic differential equations or Ordinary differential equations) within constrained time steps. These transitions of the markov chain are achieved via gradual adding of gaussian noise to the original distribution gradually destroying the structure to a pure gaussian distribution and thereafter a reverse diffusion process approximating score function via neural networks (i.e., the modeling of dynamical system) and achieving the denoising within finite steps. In my research we used the latent variation (much more stable !) wherein we utilized Tensor Train (TT) Network latent spaces to generate spatio-temporal dynamical evolution of game plays. The project introduced multidisciplinary activities wherein to generate game plays data was generated via Reinforcement learning. Achieving upto 75% reduction in parameter count !!

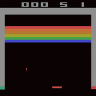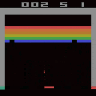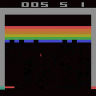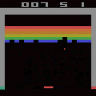
Heuristic Optimization

Performing data assimilation is a unique challenge wherein, within the assimilation window, when forming the optimization problem for an overdetrmined system (with in-situ measurements available at discrete temporal locations) leads to few different issues 1) Gradient based methods don’t work with high fidelity simulations models as their analytical gradients aren’t readily accessible (which would consequently require other time intensive numerical method, which also might be innacurate) or 2) Functions maybe discontinuos or discrete hence gradient based approaches doesn’t work 3) they are computationally expensive 4) the optimization function may introduce several local minima and the parameters inferred from a better minima might always not be physical and requires the domain knowledge to make definitive selections. Hence in my research I came up with a novel clustering based heuristic algorithm that changes a single-objective optimization problem to a multi-objective optimization problem inferring all the respective parameter combinations. Currently working on the publications, more details on the algorithm proposed would be shared there.

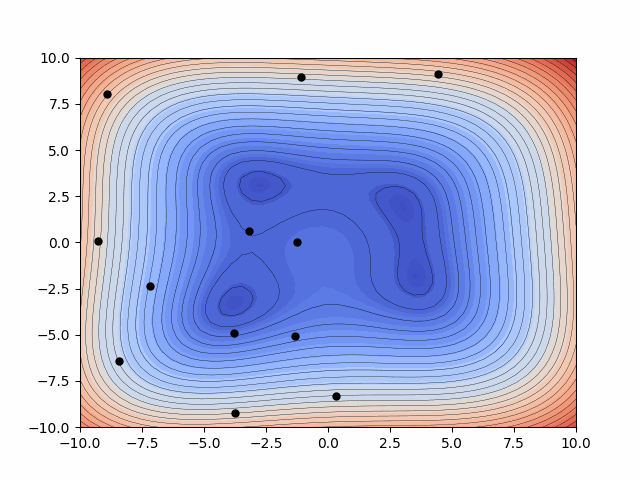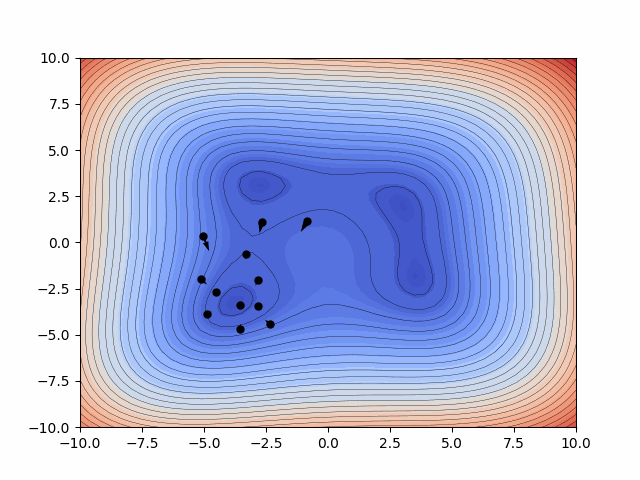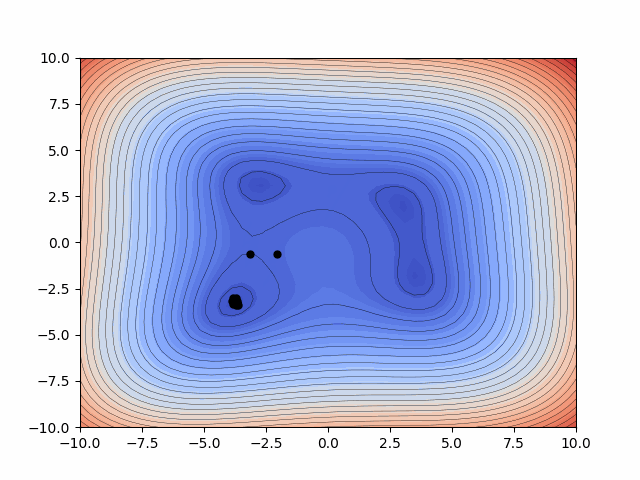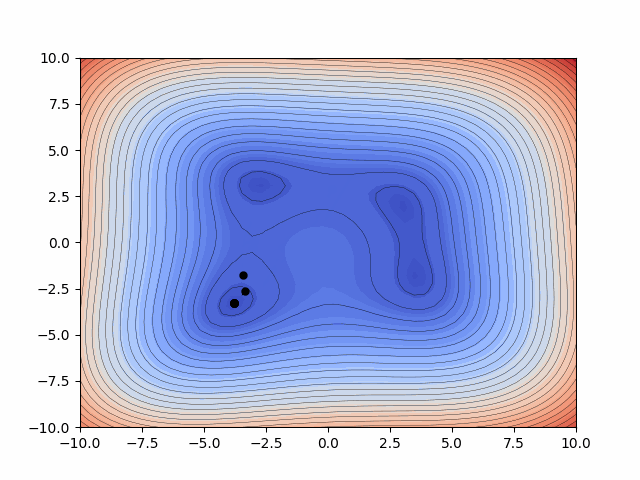
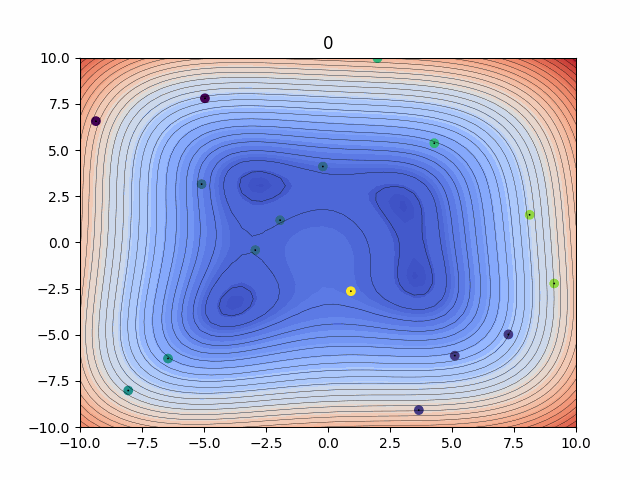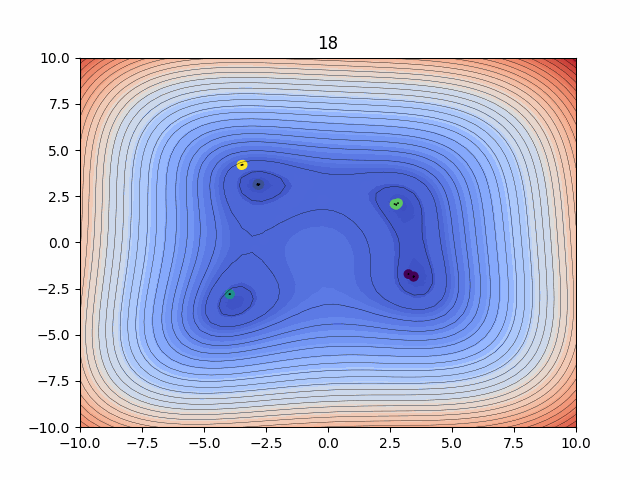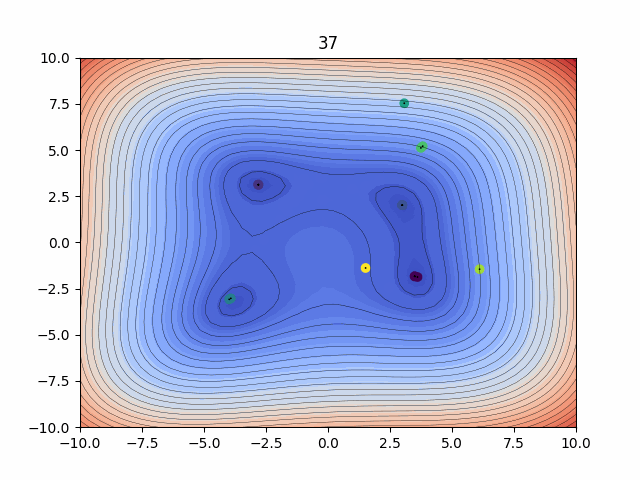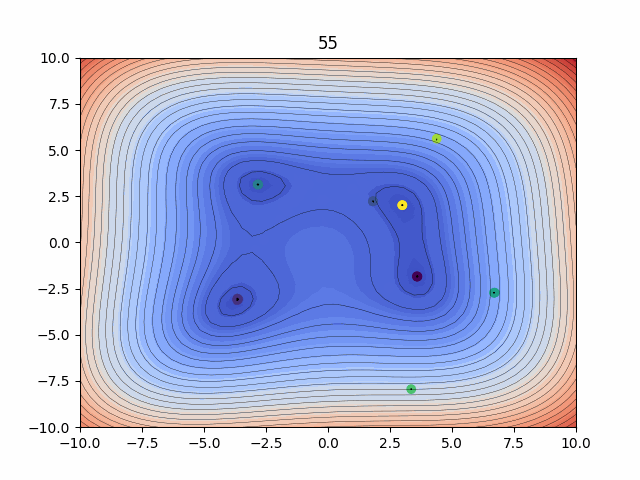
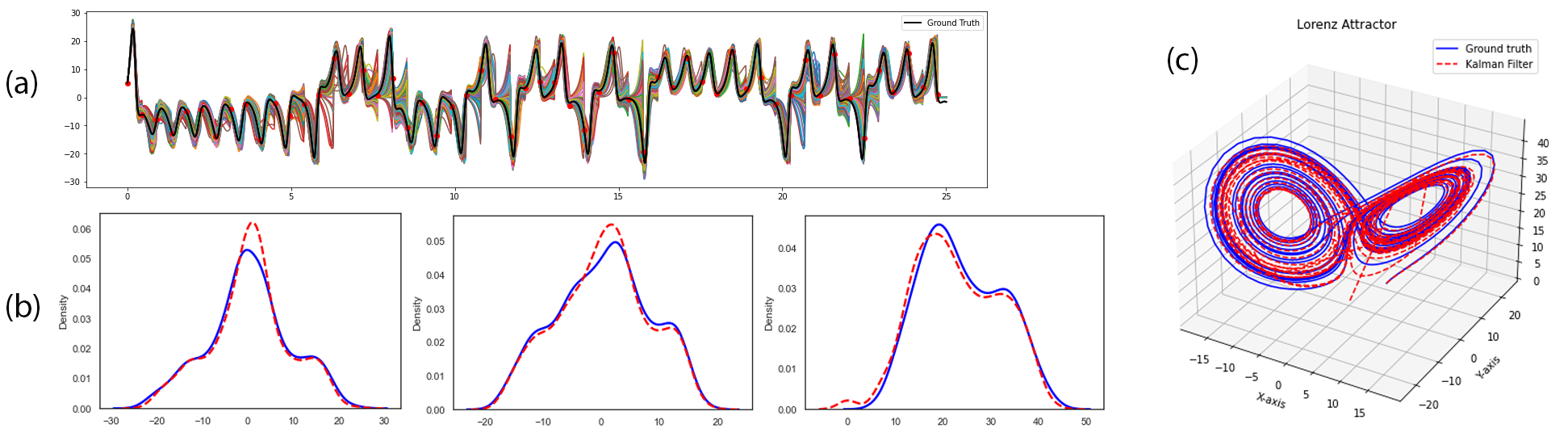
Probabilitic Inference - Kalman Filtering

The Ensemble Kalman Filters (EnKFs) and Ensemble square-root Kalman Filters (EnSRKFs) are recursive Bayesian filters based on gaussian probability distribution assumptions which are similar to particle filters wherein instead of particles here we consider ensemble members. These filters are highly scalable for problems in the context of dimensionality of the dynamical system considered since no storage and separate computation of covariance is needed and the sample covariance can be computed from the ensemble propagated in time. These algorithms hence can be utilized to improve our knowledge of both our state and parameters with the respective uncertainty aware predictions.

2. Deep learning and Chaotic dynamical systems

Chaotic systems exhibit extreme sensitivity to the initial conditions, which makes it a challenging problem coupled with the range of spatio-temporal characteristics exhibited by the system. These complexities in the dynamics of forecasting/prediction of complex systems are often encountered in various scientific disciplines and are also in their nascent stages for the exploration of machine learning as the gateway. The universality of the deep-learning framework being able to approximate a continuous function (within a specified range) in such cases, i.e. time series problems, raises the idea of being able to formulate an autonomous dynamical system. Hence, so far I have explored the following:

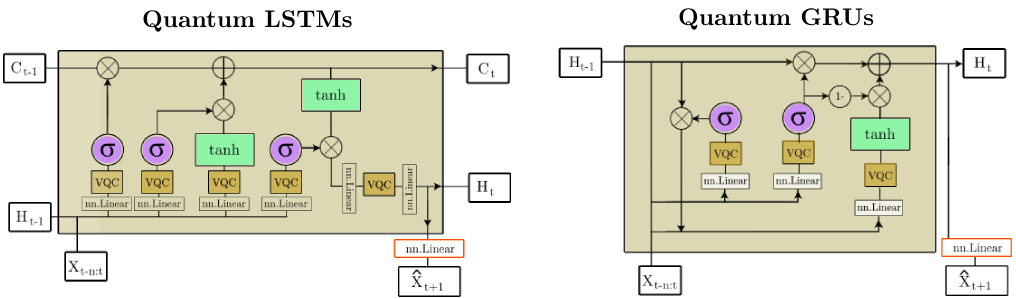
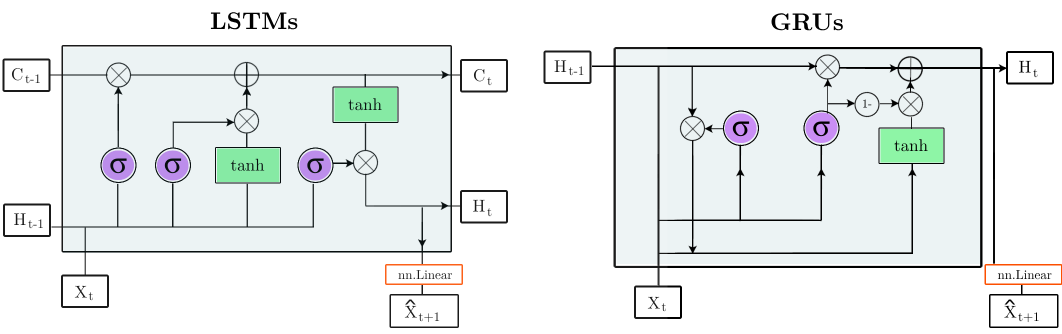
Quantum gated recurrent neural networks (MSc Thesis @ Imperial College London)

I am currently investigating Quantum machine learning algorithms and their ability to tackle chaotic dynamical systems in a teacher forced setting. The work introduces Quantum LSTMs and Quantum GRUs. So far we benchmarked these model on a simple yet tricky toy problem, i.e. sine trigonometric function, which was used as a benchmark to generalize the comparison from an interpretability standpoint. The better expressiveness of the quantum versions of LSTMs & GRUs was observed with faster convergence, robustness to the varying level of gaussian noise within data and way less parameter count compared to classical versions to achieve same MSE loss with the constraint on epochs.

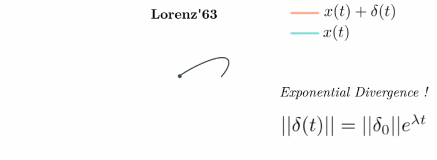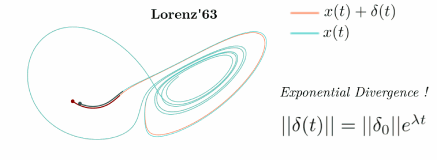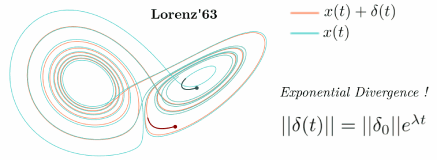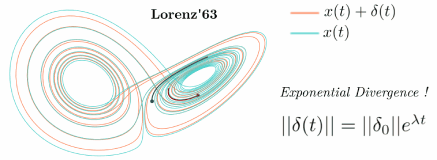
Classical gated recurrent neural networks - An autonomous dynamical system !

In this work classical deep-learning frameworks, i.e. gated recurrent neural networks (LSTMs & GRUs) were used to formulate an autonomous chaotic dynamical system. The chaotic dynamical systems used for this purpose were Lorenz’63 and Lorenz’96 system. A novel methodical foundation was laid out for the architectural design of the problem statement, and robust hyper-parameters optimization was carried out via Recycle validation and Bayesian optimization with TPE sampling. The methodology proposed was tested extensively for various metrics, i.e. accurate predictions of (i) the probability density functions (PDFs) of the DOFs, (ii) spectral properties visualized via Discrete Fourier transform (DFT) analysis, (iii) Capturing of the Prediction horizon in terms of the first few Lyapunov times and the stability of the chaotic system in terms of the (iv) Leading Lyapunov exponent computation. The outcomes of the research will be published soon !

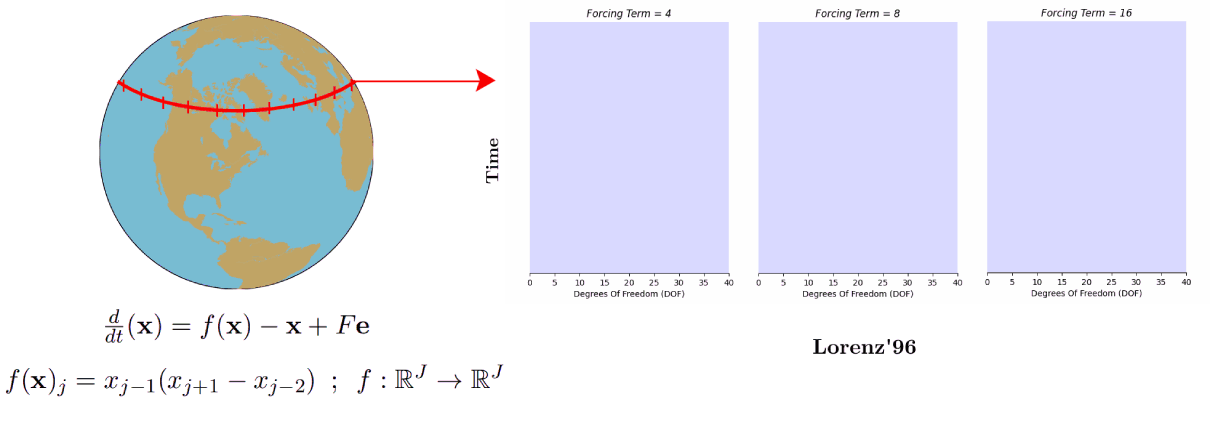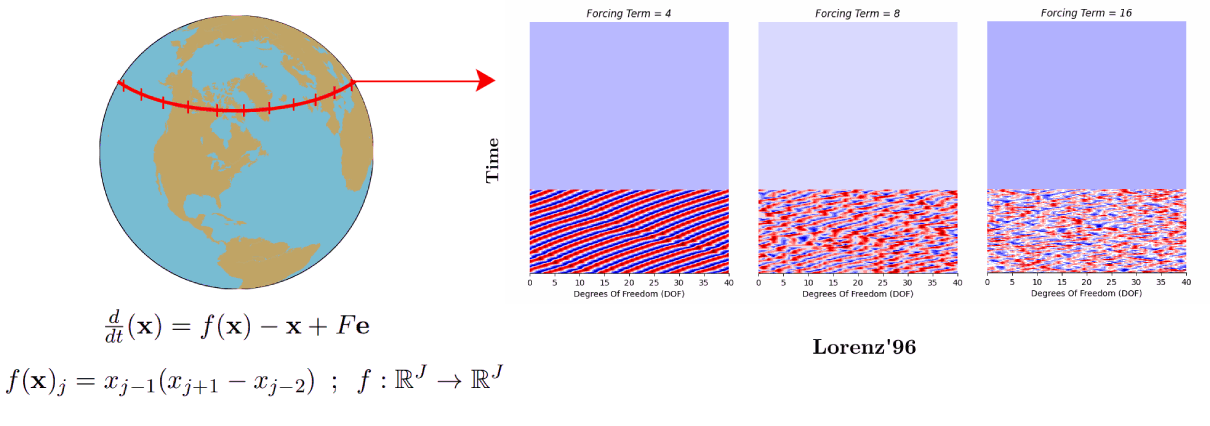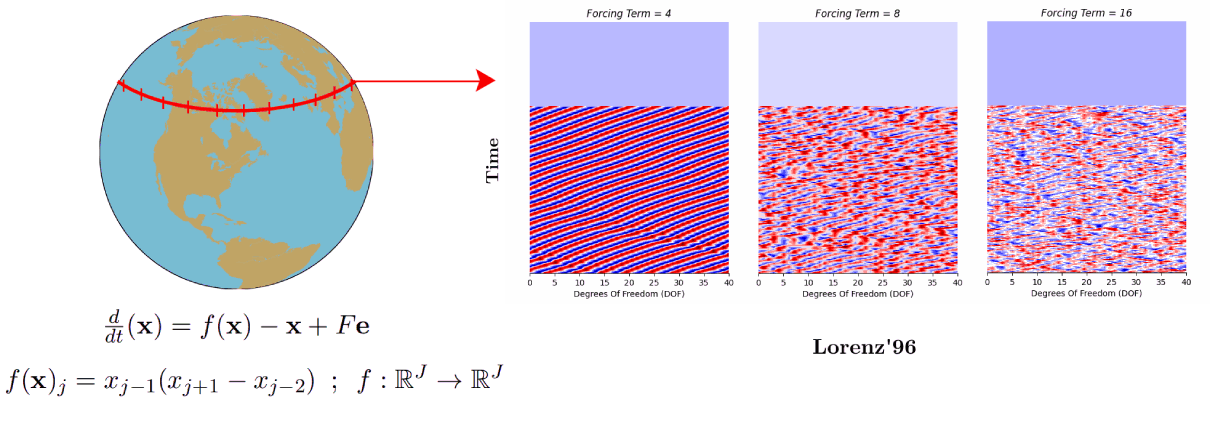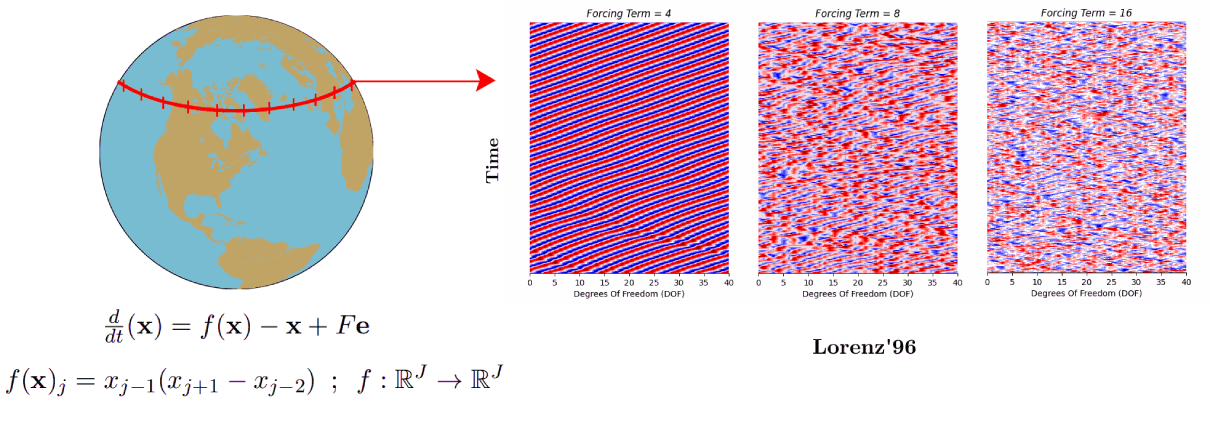
3. Deep learning and Reduced order models (ROMs)

Physics based high-fidelity predictions demand high spatio-temporal resolutions, which often leads to the mathematical modeling of large scale complex non-linear phenomenas into a high degree of freedom (DOF) dynamical system. However, conventional numerical methods used to develop dicretized solutions, give rise to increased utilization of computational resources which is often prohibitive. Hence, one of the objectives of my research is to develop deep learning based models that project these high-dimensional space to a lower dimensional space/manifold, wherein the reduced representation is the projection of the large scale physical features, with minimum loss.

State estimation using deep learning - Leveraging reduced order models (ROMs)

State estimation problems are one of the paramount application areas, that is well-established in fluid mechanics, and is often used in the applied subjects of design optimization and active flow control. In this work we try to leverage reduced order models (ROMs) as an effecient mediator to protect loss of information and a computational cheaper alternative. In this work, we proposed a novel deep learning-based state estimation framework that learns from sequential sensory data placed around the circumference of the 2D cylinder. A feedforward neural network based auto-encoder was used as an ROM to project high-dimensional space to the low-order manifold where LSTMs are used for the teacher-forced evolution of the low-order manifold taking sequential sensory data as input. More details about this work can be found [here].

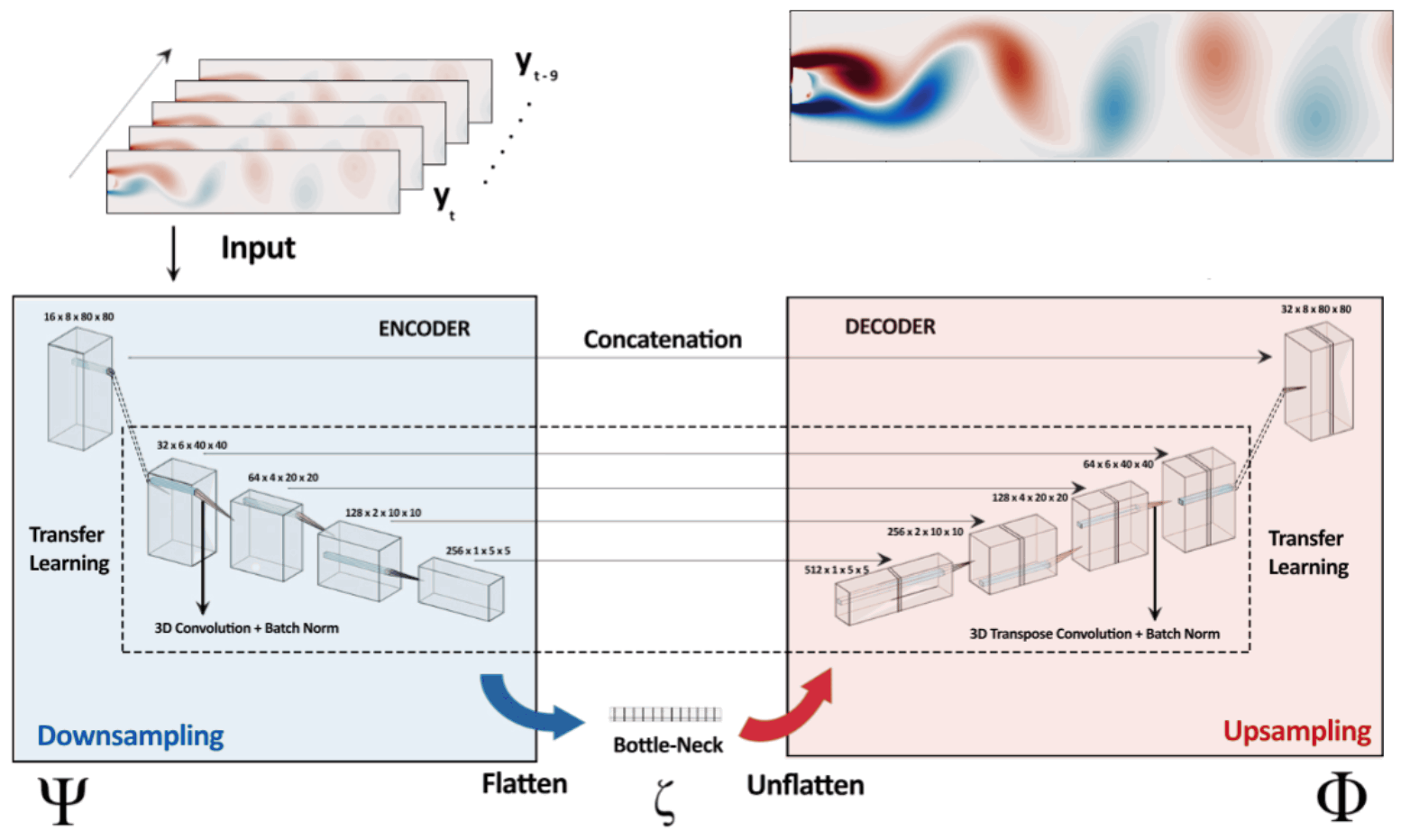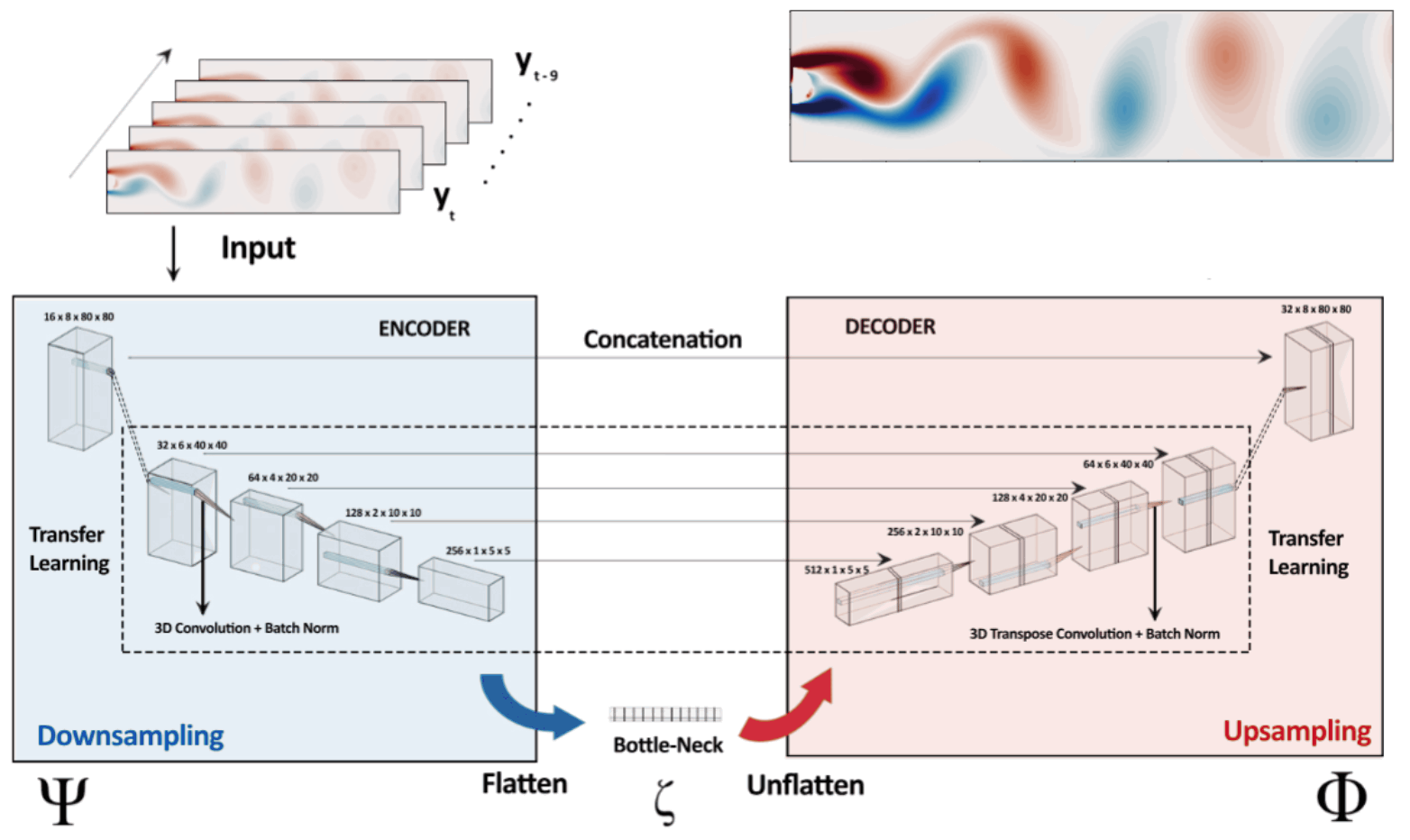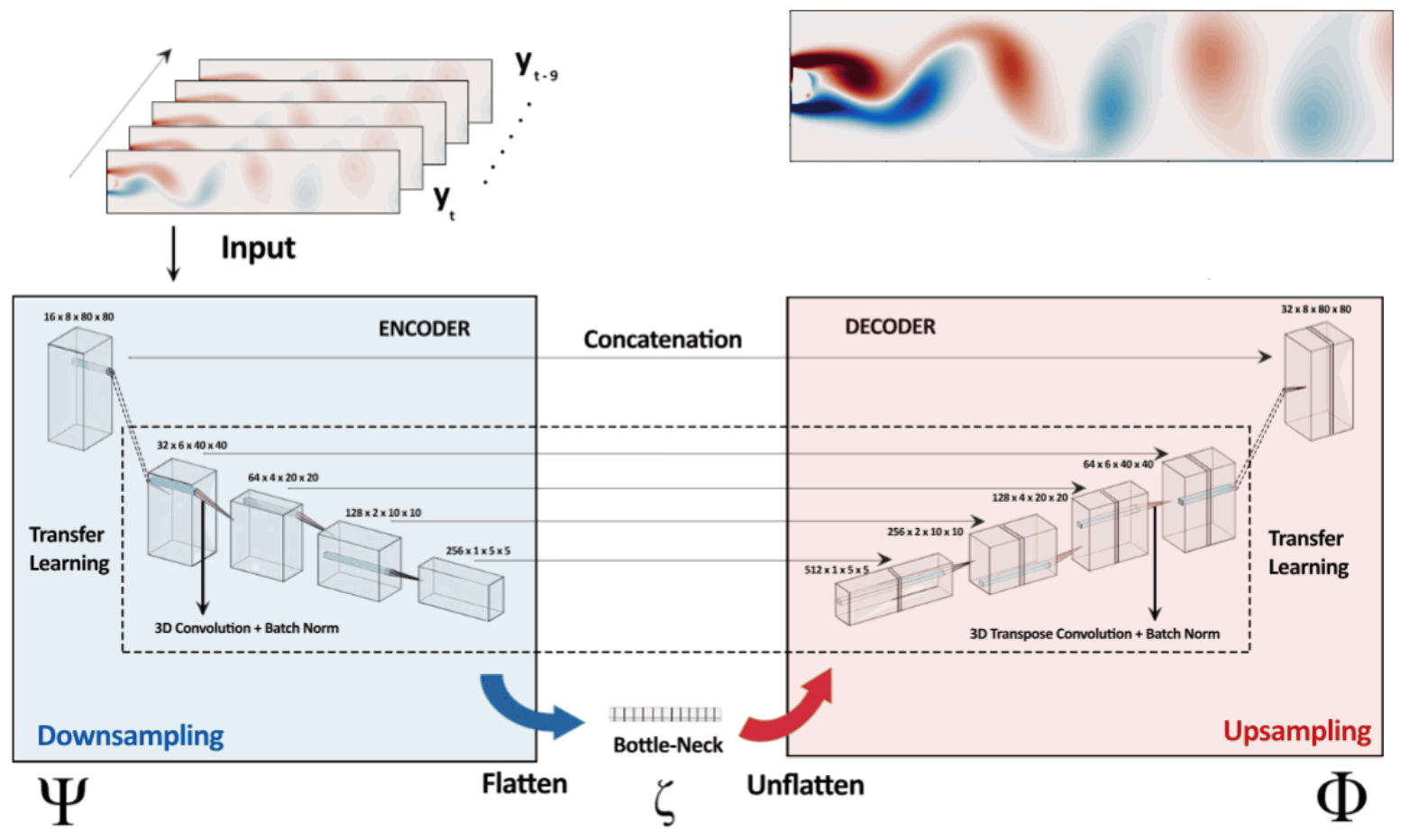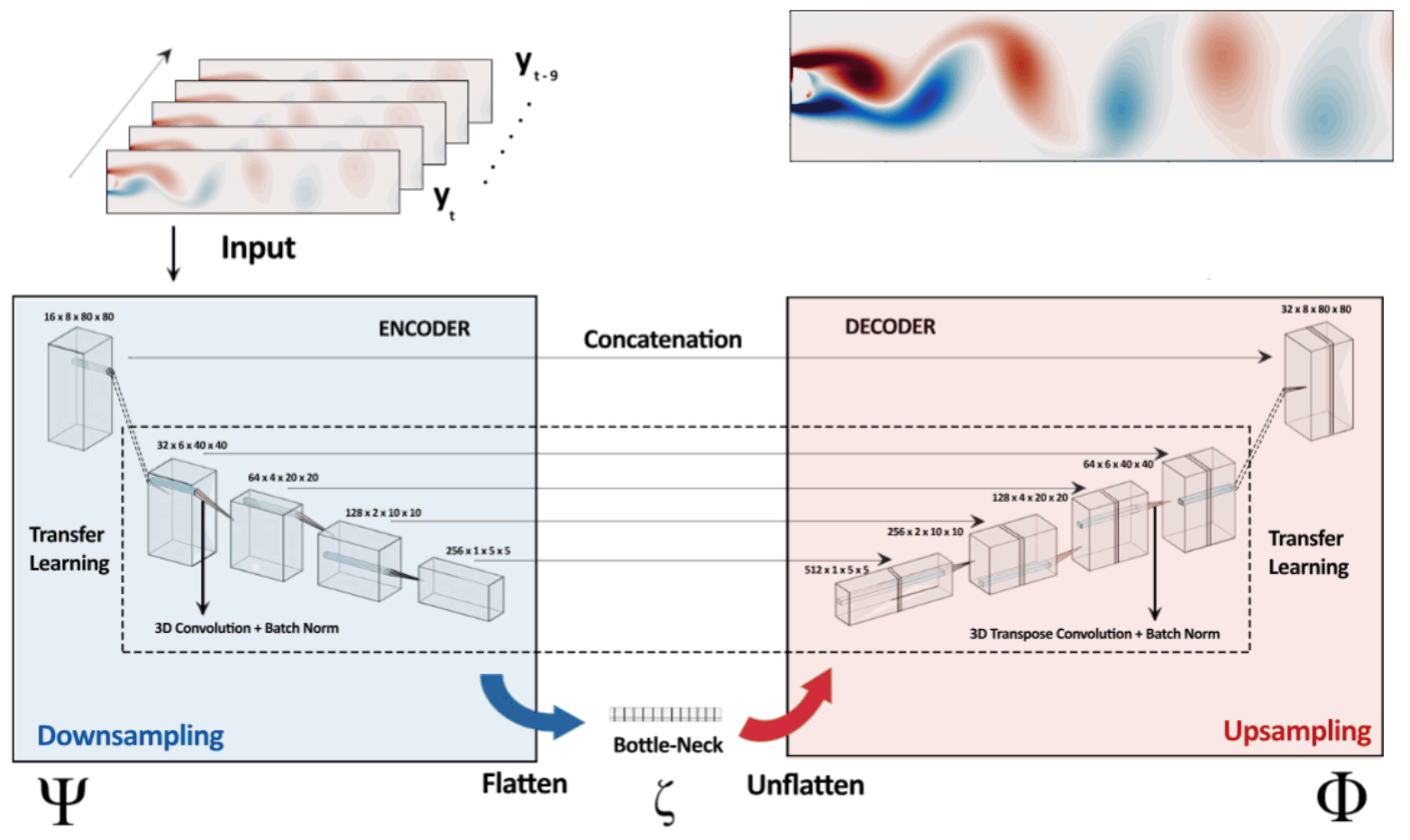
Deep learning based effecient data-driven reduced-order model (ROMs) for temporal evolution

In this work we develop a novel deep learning framework DL-ROM (deep learning—reduced order modeling) which is based on a 3D-Unet convolution network capable of performing non-linear projections to reduced order states which is further projected back to the future state of the system, thereby forming a dynamical system. Conventionally ROMs in the literature focussed on linear projection of the higher-order manifolds to lower-dimensional space using dimensionality reduction techniques which often results in loss of information. However, in this work we show, DL-ROM can create highly accurate reconstructions from the low-order manifold and is thus able to efficiently predict future time steps by temporally traversing in the learned reduced state. More details about this work can be found [here]

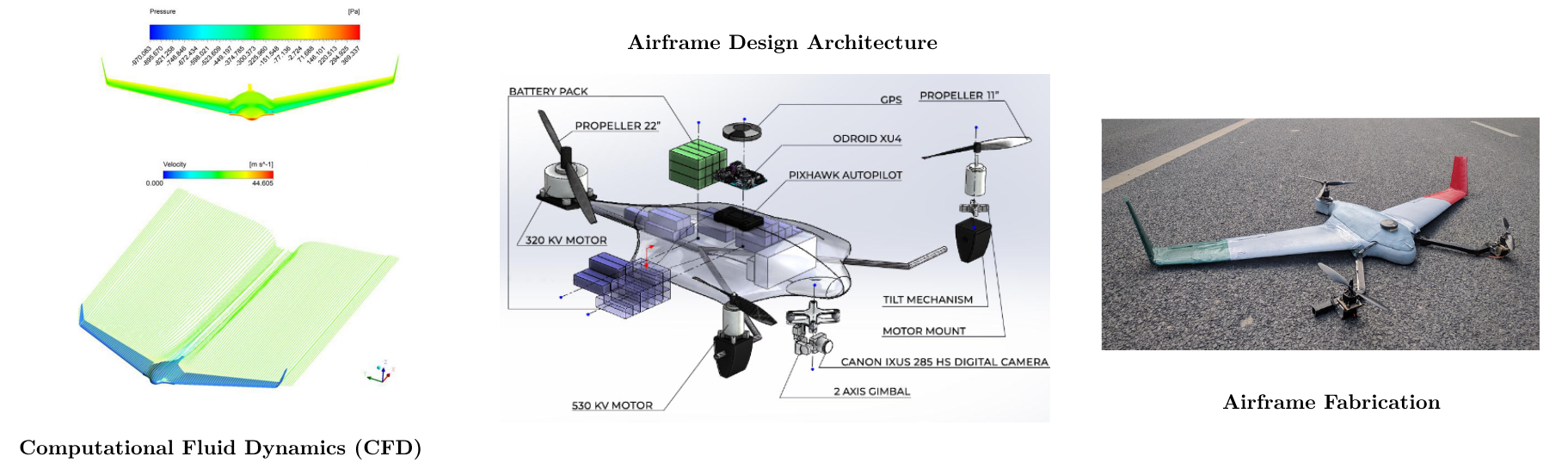
4. Unmanned Aerial Vehicles

Fabricated state-of-the-art, all-composite, Vertical Take Off and Landing Unmanned aerial vehicle (VTOL-UAV) with automatic tilt rotor mechanism using Vacuum Bagging process for HADR missions (Mehar Baba Prize competition). Improved the aerodynamic efficiency (Lift/Drag Ratio) of VTOL-UAV by introducing C-curve wing-lets by 10%, thereby enhancing the crashworthiness of the system. Developed the 3D CAD model of the UAV and tilt rotor mechanism on Solidworks. Carried out 3D CFD Simulations using K-omega turbulence model to evaluate the Coefficient of lift and drag of the VTOL-UAV. Numerical experiments were performed on ANSYS Fluent and OpenFOAM.

Selected Course Projects

Computational Fluid Dynamics

• Implementation of second & fourth order accurate finite difference schemes for 2D Laplace Equation.
• Implementation of a finite-difference FORTRAN code using Adams-Bashforth and Runge-Kutta numerical schemes for 2D compressible Navier-Stokes equations (Flow around cylinder) with periodic boundary conditions.
• Carried out 2D/3D CFD simulations around airfoils via vortex lattice method (VLM), Reynolds-averaged Navier–Stokes (RANS) [Turbulence Models: Spallart allamaras, K-Omega SST, k-epsilon] and Spectral/Hp Element Methods via softwares XFOIL, StarCCM+ and Nektar++ respectively.

Computational Linear Algebra and Machine Learning

• Implementation of partial/complete pivoting LU factorization algorithms for discretized integral equations.
• Support vector machine (SVM) for NASA asteroid classification.
• Convolution NNs for prediction of angle of attack (AoA) of airfoils from 2D snapshots.
• Feedforward neural networks to predict mechanical properties of fibre composites.
• LSTMs for the predictions of air speed based on sequential data from the hot wire measurements in a wind tunnel.